Базовая логика

• Logic gates
  • Законы де Моргана: Позволяют упрощать и инвертировать сложные условия
  • AND
  • OR
  • XOR (Исключающее ИЛИ)
  • NOT
  • NAND
  • NOR (ИЛИ-НЕ)
  • XNOR
• Always ON
• Second tick
• XOR элемент
• OR gate with 3 inputs
• AND gate with 3 inputs

Logic gates

Логические вентили можно комбинировать для решения более сложных задач, например для выполнения простых арифметических операций.

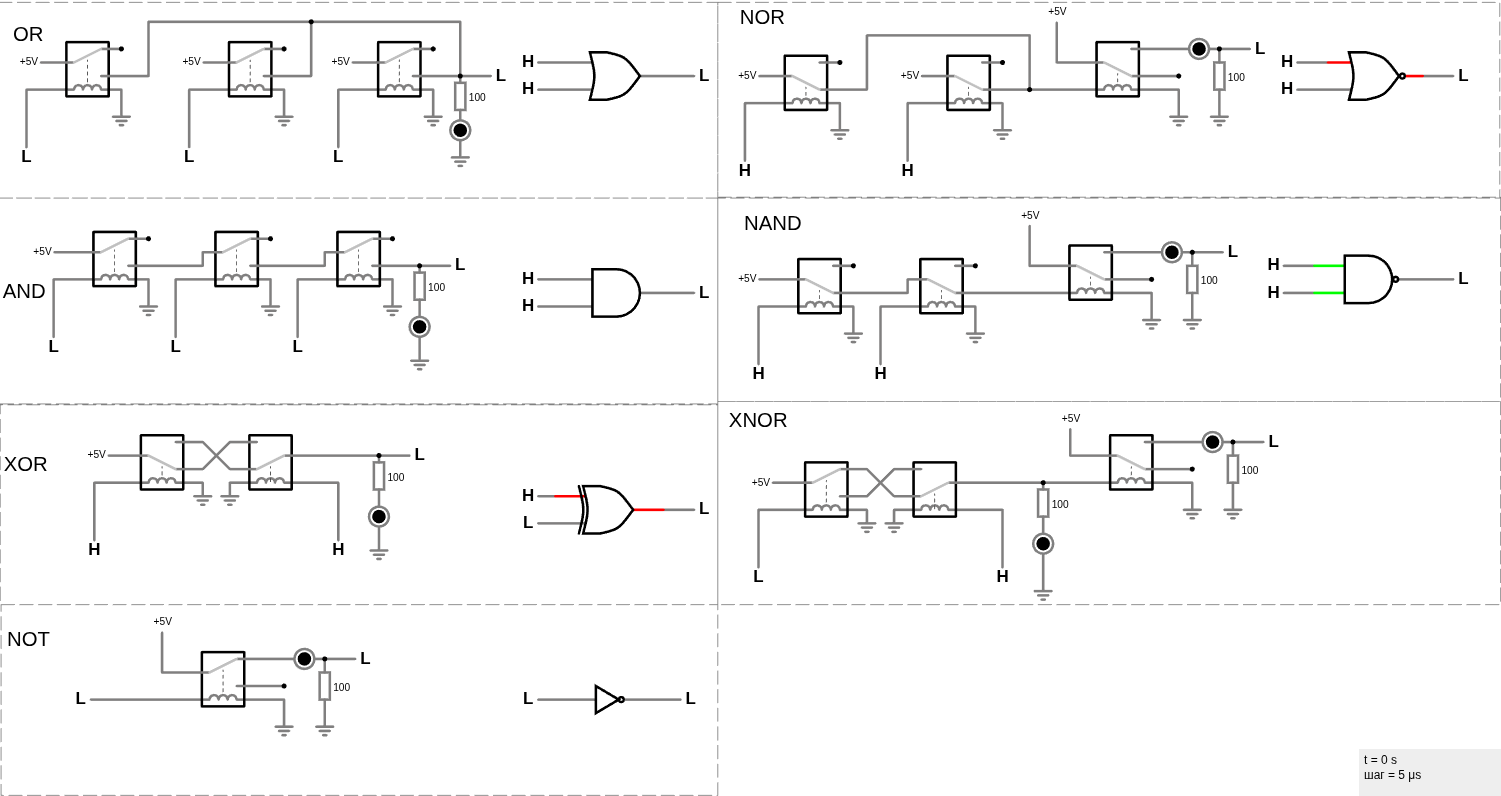
Логические вентили с помощью реле (www.falstad.com/circuit)

Логические вентили на современной логике CMOS: MOSFET (P-MOSFET/P-MOS и N-MOSFET/N-MOS)

Как работают логические элементы (learnabout-electronics.org)

P-MOS транзисторы используются в качестве подтягивающих резисторов, а N-MOS транзисторы — в качестве понижающих. Благодаря этому статическое энергопотребление логических элементов и схем на основе КМОП-технологии очень низкое по сравнению с логическими элементами, разработанными с использованием только N-MOS или только P-MOS транзисторов

P-MOS и N-MOS получают одинаковые управляющие сигналы, но работают инверсно

Именно эта комплементарность (Complementary) дала название CMOS — Complementary MOS.

N-MOSFET:

• Открывается при HIGH (1) на Gate (GND проходит на Drain)
• Закрывается при LOW (0) на Gate
• Хорошо проводит 0V (GND)
• Плохо проводит Vdd (потери Vth)
• Body (подложка) подключается к GND

P-MOSFET:

• Открывается при LOW (0) на Gate (Source проходит на Drain)
• Закрывается при HIGH (1) на Gate
• Хорошо проводит Vdd (+5V)
• Плохо проводит GND (потери Vth)
• Body подключается к Vdd

Body всегда к своему питанию (P-MOS к Vdd, N-MOS к GND)

В общем случае, любой логический элемент на основе КМОП-технологии состоит из повышающей и понижающей цепей. Повышающая цепь состоит из PMOS-транзисторов, а понижающая — из NMOS-транзисторов. Входы обеих цепей одинаковы.

Принцип работы КМОП-инвертора:

Когда входной сигнал логический «0», PMOS-транзистор будет включен, а NMOS-транзистор — выключен. Поэтому выход будет подключен к 5 В. Более того, поскольку PMOS-транзистор пропускает сильную логическую «1», выходное напряжение будет очень близко к напряжению питания.

С другой стороны, когда Vin равен логической «1», PMOS-транзистор будет выключен, а NMOS-транзистор — включен. В этом случае NMOS-транзистор понизит выходное напряжение до логического «0». А поскольку NMOS-транзистор пропускает сильный «0», выходное напряжение будет очень близко к 0 В.

Таким образом, в любой момент времени либо PMOS-транзистор включен, либо NMOS-транзистор включен. И нет прямого пути от источника питания к земле. И поэтому статическое энергопотребление логического элемента CMOS практически пренебрежимо мало.

Законы де Моргана: Позволяют упрощать и инвертировать сложные условия.

Булева алгебра (learnabout-electronics.org)

Исходное тождество !(A && B) эквивалентно ≡ !A || !B

• Если теперь отрицать обе части, получим:
  • !(!(A && B)) ≡ !(!A || !B)
  • убираем двойное отрицание слева, получим:
  • A && B ≡ !(!A || !B)

Исходное тождество !(A || B) ≡ !A && !B

• Если теперь отрицать обе части, получим:
  • A || B ≡ !(!A && !B)

AND — A && B

AND в логике и программировании означает И (логическое умножение или конъюнкция). Это логическая операция, которая выдает истину (True), только если оба операнда истинны. Если хотя бы один из операндов ложен, то результат — ложь. Так же объединение NAND + NOT эквивалентно AND.

• AND можно получить через NAND A && B ≡ !(A NAND B)
• AND можно получить через NOR A && B ≡ !(!A || !B) ≡ (A NOR A) NOR (B NOR B)

Таблица истинности для логического элемента AND

Таблица истинности для логического элемента AND с тремя входами (A), (B), (C):

$Y=A\wedge B\wedge C$

const NAME_WIDTH: usize = 4;
fn print_truth_table(name: &str, gate: fn(u8, u8) -> u8) {
    println!("|{:^width$}| 0 | 1 |", name, width = NAME_WIDTH);
    println!("|{:-^width$}|---|---|", "", width = NAME_WIDTH);

    for b in 0..=1 {
       println!(
           "|{:^width$}| {} | {} |",
           b,
           gate(0, b),
           gate(1, b),
           width = NAME_WIDTH
       );
    }
    println!("");
}

fn or(a: u8, b: u8) -> u8 { a | b }
fn not(x: u8) -> u8 {!x & 1}

fn and(a: u8, b: u8) -> u8 {
    a & b
}

fn and_by_using_or(a: u8, b: u8) ->u8{
    not(or(not(a),not(b)))
}

fn main() {
    print_truth_table("AND", and);

    print_truth_table("AND", and_by_using_or);
}

Варианты реализации логики gate AND

OR — A || B

OR это логическая операция, которая выдает истину (True), если хотя бы один из операндов истинен. Мат. синтаксис A + B

• OR можно получить через AND (A || B) ≡ !(!A && !B)
• OR можно получить через NAND (A || B) ≡ (A NAND A) NAND (B NAND B)
• OR можно получить через NOR (A || B) ≡ !(!(A || B))

Таблица истинности для логического элемента OR

Таблица истинности для логического элемента OR с тремя входами:

$Y=A\vee B\vee C$

const NAME_WIDTH: usize = 4;
fn print_truth_table(name: &str, gate: fn(u8, u8) -> u8) {
    println!("|{:^width$}| 0 | 1 |", name, width = NAME_WIDTH);
    println!("|{:-^width$}|---|---|", "", width = NAME_WIDTH);

    for b in 0..=1 {
       println!(
           "|{:^width$}| {} | {} |",
           b,
           gate(0, b),
           gate(1, b),
           width = NAME_WIDTH
       );
    }
    println!("");
}
fn and(a: u8, b: u8) -> u8 { a & b }
fn nand(a: u8, b: u8) -> u8 { not(a & b)}
fn not(x: u8) -> u8 { !x & 1 }

fn or(a: u8, b: u8) -> u8 {
    a | b
}
 
fn or_by_using_and(a: u8, b: u8) -> u8 { 
    not(and(not(a),not(b)))
}

fn or_by_using_nand(a: u8, b: u8) -> u8 { 
    nand(nand(a, a), nand(b, b))
}

fn main() {
    print_truth_table("OR", or);
    print_truth_table("OR", or_by_using_and);    
    print_truth_table("OR", or_by_using_nand);
}

Варианты реализации логики gate OR

XOR — A XOR B

XOR (от англ. Exclusive OR/Исключающее ИЛИ). Это логическая операция, которая выдает истину (True), если только один из операндов истинен, и ложь (False), если оба операнда одинаковы (оба истинны или оба ложны). Математически записывается как $Y=A\oplus B$

• XOR можно получить через AND + OR + NOT: A XOR B = (A && !B) || (!A && B)
• XOR можно получить через NAND: A XOR B = (A NAND (A NAND B)) NAND (B NAND (A NAND B))
• XOR можно получить через NOR: A XOR B = (A NOR B) NOR ((A NOR A) NOR (B NOR B))
• XOR можно получить через NAND + AND + OR: A XOR B = (A NAND B) && (A || B)

const NAME_WIDTH: usize = 4;
fn print_truth_table(name: &str, gate: fn(u8, u8) -> u8) {
    println!("|{:^width$}| 0 | 1 |", name, width = NAME_WIDTH);
    println!("|{:-^width$}|---|---|", "", width = NAME_WIDTH);

    for b in 0..=1 {
       println!(
           "|{:^width$}| {} | {} |",
           b,
           gate(0, b),
           gate(1, b),
           width = NAME_WIDTH
       );
    }
    println!("");
}

fn and(a: u8, b: u8) -> u8 { a & b }
fn or(a: u8, b: u8) -> u8 { a | b }
fn nand(a: u8, b: u8) -> u8 { 
  not(a & b)  
}
fn not(x: u8) -> u8 {!x & 1}

fn xor(a: u8, b: u8) -> u8 {
    a ^ b
}
 
fn xor_by_using_nand_and_or(a: u8, b: u8) -> u8 {
    and(nand(a, b), or(a, b))
}

fn main() {
    print_truth_table("XOR", xor);
    print_truth_table("XOR", xor_by_using_nand_and_or);    
}

Для понимания предела цифровой абстракции (когда нам не важен шум и паденение напряжения у различных компонентов, у нас есть только высокий HIGH и низкий LOW уровень) мы должны рассмотреть поведение логических элементов с аналоговой точки зрения. Передаточная характеристика (DС transfer characteristics) какого-либо логического элемента описывает напряжение на выходе этого элемента как функцию напряжения на его входе, когда входной сигнал изменяется настолько медленно, что выходной сигнал успевает изменяться вслед за ним.

import numpy as np
import matplotlib.pyplot as plt

# Параметры типичного 3В CMOS элемента
V_DD = 3.0
V_IL, V_IH = 1.0, 2.0  # Входные пороги
V_OL, V_OH = 0.2, 2.8  # Выходные пороги
k = 12                 # Крутизна

v_range = np.linspace(0, V_DD, 100)

# 1. Подготовка данных для 2D среза (фиксация B = V_DD для XOR)
# При B = 3В, XOR превращается в инвертор для входа A
A_2d = v_range
sig_A = 1 / (1 + np.exp(-k * (A_2d - (V_DD/2))))
Y_2d = V_DD * (1 - sig_A) # Инвертированное поведение

# Создание графиков
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(14, 6))

# --- ПРАВЫЙ ГРАФИК: 2D Срез с уровнями ---
ax2.plot(A_2d, Y_2d, 'b', lw=3, label='Передаточная характеристика')

# Отмечаем области
ax2.axhspan(V_OH, V_DD, color='green', alpha=0.1, label='Зона HIGH (Выход)')
ax2.axhspan(0, V_OL, color='red', alpha=0.1, label='Зона LOW (Выход)')
ax2.axvspan(0, V_IL, color='gray', alpha=0.2, label='Допустимый LOW на входе')
ax2.axvspan(V_IH, V_DD, color='gray', alpha=0.4, label='Допустимый HIGH на входе')

# Точки порогов
ax2.annotate(f'V_IL={V_IL}V', xy=(V_IL, 2.5), rotation=90, va='bottom')
ax2.annotate(f'V_IH={V_IH}V', xy=(V_IH, 0.5), rotation=90, va='bottom')
ax2.annotate(f'V_OH={V_OH}V', xy=(0.2, V_OH), va='bottom')
ax2.annotate(f'V_OL={V_OL}V', xy=(2.2, V_OL), va='bottom')

ax2.set_title('2D Срез (A меняется, B=3В)')
ax2.set_xlabel('Входное напряжение V_in (A)')
ax2.set_ylabel('Выходное напряжение V_out (Y)')
ax2.grid(True, linestyle='--')
ax2.legend(loc='upper right', fontsize='small')

# --- ЛЕВЫЙ ГРАФИК: 3D Поверхность (для контекста) ---
from mpl_toolkits.mplot3d import Axes3D
ax1 = fig.add_subplot(121, projection='3d')
A_m, B_m = np.meshgrid(v_range, v_range)
sA = 1 / (1 + np.exp(-k * (A_m - 1.5)))
sB = 1 / (1 + np.exp(-k * (B_m - 1.5)))
Y_m = V_DD * (sA * (1 - sB) + (1 - sA) * sB)

# Добавлены параметры edgecolor, linewidth и шаг сетки (rcount, ccount)
ax1.plot_surface(A_m, B_m, Y_m, cmap='magma', alpha=0.8, 
                 edgecolor='black', linewidth=0.3, rcount=30, ccount=30)

ax1.set_title('3D XOR Характеристика')
ax1.set_xlabel('A')
ax1.set_ylabel('B')
ax1.set_zlabel('Y')
ax1.view_init(elev=20, azim=-135)

plt.tight_layout()
plt.show()

Как читать этот график:

1. Серые вертикальные зоны ($V_{IL},V_{IH}$): Это границы «дозволенного» для входного сигнала. Если Вы подаете напряжение в белую зону между ними, Вы попадаете в область неопределенности, где логика может сбоить.
2. Цветные горизонтальные зоны ($V_{OL},V_{OH}$): Это «обещания» элемента. Вы видите, что график (синяя линия) заходит глубоко в эти зоны. Это означает, что элемент выдает очень качественный сигнал, который с запасом перекрывает требования следующего за ним элемента.
3. Запас помехоустойчивости: Расстояние между границей серой зоны ($V_{IL}$) и фактическим выходом в красной зоне ($V_{OL}$) — это и есть тот самый физический «буфер», защищающий от ошибок.

Анализ графика:

• Точка (A=0, B=0): Выход $Y\approx 0$ (Низкий уровень).
• Точка (A=3, B=0): Выход $Y\approx 3$ (Высокий уровень).
• Точка (A=0, B=3): Выход $Y\approx 3$ (Высокий уровень).
• Точка (A=3, B=3): Выход $Y\approx 0$ (Низкий уровень).

Передаточная характеристика как раз проводит границу: до какого момента мы можем игнорировать аналоговую природу сигнала (шум, падение напряжения) и продолжать считать его «цифровым». Передаточная характеристика показывает нам ширину «мертвой зоны» (переходного региона), и чем круче наклон графика в этой зоне, тем лучше логический элемент восстанавливает чистоту цифрового сигнала.

Зачем она нужна? Она позволяет инженерам увидеть не просто абстрактные «0» и «1», а реальное физическое поведение устройства

• Пороговые напряжения: При каком именно значении входного сигнала «0» превращается в «1»?
• Помехоустойчивость: Насколько сильно можно изменить (зашумить) входной сигнал, чтобы выход при этом остался стабильным.
• Линейность: Насколько плавно или резко происходит переход между состояниями.

В теории: Логический элемент должен переключаться мгновенно. График выглядел бы как идеальная «ступенька».

На практике: Как вы видите на рисунке, у «стенки» графика есть наклон. Это переходная область, где транзисторы внутри элемента находятся в активном режиме, и сигнал не является ни чистым нулем, ни чистой единицей.

NOT — !A

NOT (Инвертор) Инвертирует входное значение. Истина становится Ложью, и наоборот.

0 -> NOT -> 1

1 -> NOT -> 0

// Операция &1 означает нормализовать 8 бит к 0 или 1 
// т.е. оставить только младший бит, всё остальное выбросить
// Для типа bool нормализация не нужна
fn not(x: u8) -> u8 {
  !x & 1
}
 
fn main() {
    assert_eq!(not(1),0);
    assert_eq!(not(0),1);    
}

NAND — !(A && B)

NAND (Not-AND/И-НЕ) Противоположность AND. Выдает Ложь, только если оба входа Истинны. Т.е. сперва применяется операция AND и к результату ее применяется операция NOT: 1 AND 1 = 1 NOT = 0

Из AND можно получить NAND и наоборот:

• NAND можно получить через AND, так как A && B ≡ !(A NAND B)
• NAND можно получить через OR !(A && B) ≡ (!A) || (!B)
  • 
• NAND можно получить через NOR !(A && B) ≡ (A NOR A) OR (B NOR B)

const NAME_WIDTH: usize = 4;
fn print_truth_table(name: &str, gate: fn(u8, u8) -> u8) {
    println!("|{:^width$}| 0 | 1 |", name, width = NAME_WIDTH);
    println!("|{:-^width$}|---|---|", "", width = NAME_WIDTH);

    for b in 0..=1 {
       println!(
           "|{:^width$}| {} | {} |",
           b,
           gate(0, b),
           gate(1, b),
           width = NAME_WIDTH
       );
    }
    println!("");
}

fn and(a: u8, b: u8) -> u8 { a & b }
fn or(a: u8, b: u8) -> u8 { a | b }
fn nor(a: u8, b: u8) -> u8 { not(a | b) }
fn not(x: u8) -> u8 {!x & 1}

fn nand(a: u8, b: u8) -> u8 { 
  not((a & b)) 
}

fn nand_by_using_and(a: u8, b: u8) -> u8 { 
  not(and(a, b))
}

fn nand_by_using_or(a: u8, b: u8) -> u8 { 
  or(not(a), not(b))  
}

fn nand_by_using_nor(a: u8, b: u8) -> u8 { 
  or(nor(a, a), nor(b, b)) 
}

fn main() {
    print_truth_table("NAND", nand);
    print_truth_table("NAND", nand_by_using_and);
    print_truth_table("NAND", nand_by_using_or);
    print_truth_table("NAND", nand_by_using_nor);
}

NOR — !(A || B)

NOR (Not-OR/ИЛИ-НЕ) Противоположность OR. Выдает Истину, только если оба входа Ложны. Т.е. сперва применяется операция OR и к результату ее применяется операция NOT: 0 OR 0 = 0 NOT = 1 Так же можно получить NOR

• NOR можно получить через AND !(A || B) ≡ (! A) && (! B)
• NOR можно получить через NAND !(A || B) ≡ (! A) && (! B) = !(!A NAND !B)

Так же можно получить NOR если инвертировать выход OR, сравните таблицу истинности, если выход NOR !(A || B) инвертировать то получим OR A || B

Таблица истинности для логического элемента NOR

Таблица истинности для логического элемента NOR с тремя входами:

$Y=\overline{A\vee B\vee C}$

Задача: вывести NOR !(A || B) имея только NAND !(A && B) и NOT !A

• по закону де Моргана
  • A || B ≡ !(!A && !B)
• тогда через его отрицание получим NOR
  • !(A || B) ≡ !(!(!A && !B))
• устраним двойное отрицание
  • !(A || B) ≡ !A && !B
• преобразуем AND в NAND
  • !(A || B) ≡ !(!A NAND !B)

const NAME_WIDTH: usize = 4;
fn print_truth_table(name: &str, gate: fn(u8, u8) -> u8) {
    println!("|{:^width$}| 0 | 1 |", name, width = NAME_WIDTH);
    println!("|{:-^width$}|---|---|", "", width = NAME_WIDTH);

    for b in 0..=1 {
       println!(
           "|{:^width$}| {} | {} |",
           b,
           gate(0, b),
           gate(1, b),
           width = NAME_WIDTH
       );
    }
    println!("");
}

fn and(a: u8, b: u8) -> u8 { a & b }
fn not(x: u8) -> u8 {!x & 1}

fn nor(a: u8, b: u8) -> u8 {
    not(a | b)
}

fn nor_by_using_and(a: u8, b: u8) -> u8 { 
    and(not(a), not(b))  
}

fn main() {
    print_truth_table("NOR", nor);
    print_truth_table("NOR", nor_by_using_and);    
 
}

XNOR — !(A ⊕ B)

XNOR (Exclusive-NOR/Исключающее ИЛИ-НЕ/NOT XOR). Противоположность XOR. Выдает Истину, если оба входа одинаковы (оба Ложны или оба Истинны).

• XNOR можно получить через XOR + NOT: !(A ⊕ B) = !(A XOR B)
• XNOR можно получить через AND + OR + NOT: !(A ⊕ B) = (A && B) || (!A && !B)
• XNOR можно получить через XOR + NAND: !(A ⊕ B) = XOR NAND XOR
• XNOR можно получить через NOR: !(A ⊕ B) = ((A NOR B) NOR ((A NOR A) NOR (B NOR B))) NOR ((A NOR B) NOR ((A NOR A) NOR (B NOR B)))

const NAME_WIDTH: usize = 4;
fn print_truth_table(name: &str, gate: fn(u8, u8) -> u8) {
    println!("|{:^width$}| 0 | 1 |", name, width = NAME_WIDTH);
    println!("|{:-^width$}|---|---|", "", width = NAME_WIDTH);

    for b in 0..=1 {
       println!(
           "|{:^width$}| {} | {} |",
           b,
           gate(0, b),
           gate(1, b),
           width = NAME_WIDTH
       );
    }
    println!("");
}

fn not(x: u8) -> u8 {!x & 1}
fn xor(a: u8, b: u8) -> u8 { a ^ b}

fn xnor(a: u8, b: u8) -> u8 {
    not(xor(a,b))  
}

fn main() {
    print_truth_table("XNOR", xnor);
}

Always ON

(Всегда включен)

Задача: Как получать на выходе всегда 1 при любом входе, имея в расспоряжении NOR, NAND, AND, OR, NOT

Один из вариантов, к результату NOR применить OR, так как их таблицы истинности наглядно показывают это поведение. Тогда мы сможем все нули NOR преобразовать в 1 через OR.

Second tick

Второй тик

Задача: Ожидаемый выход 1 только при входе A=1, B=0

... решение напоминает таблицу истинности для XOR

если для случая A=0, B=1 инвертировать результат через AND то можно получить трубуемое поведение.

Но более простой вариант это NOT + AND. Если мы вход B предварительно инвертируем, то при случаии A=1, B=0 мы инвертируем B и получим 1, а в остальных случаях результат через AND всегда будет 0

Ожидаемое поведение, таблица истинности:

A   0 1 0 1
B   0 0 1 1
out 0 1 0 0

const NAME_WIDTH: usize = 4;
fn print_truth_table(name: &str, gate: fn(u8, u8) -> u8) {
    println!("|{:^width$}| 0 | 1 |", name, width = NAME_WIDTH);
    println!("|{:-^width$}|---|---|", "", width = NAME_WIDTH);

    for b in 0..=1 {
       println!(
           "|{:^width$}| {} | {} |",
           b,
           gate(0, b),
           gate(1, b),
           width = NAME_WIDTH
       );
    }
    println!("");
}
fn and(a: u8, b: u8) -> u8 { a & b }
fn not(x: u8) -> u8 {!x & 1}

fn tick(a: u8, b: u8) -> u8 { 
    and(a, not(b))
}

fn main() {
    print_truth_table("tick", tick);
}

XOR элемент

Задача: Получить XOR

Таблица истинности XOR

OR gate with 3 inputs

(A || B) || (B || C)

AND gate with 3 inputs

(A && B) && (B && C)