Arithmetic
- Конвертация десятичных чисел в двоичные
- Double trouble
- Odd number of signals
- Counting signals
- Half Adder
- Full Adder
- Double the number
- Byte OR
- Byte NOT
- Adding Bytes
- Negative Numbers
- Signed Negator
- 1 Bit Decoder
- 3 Bit Decoder
- Logic Engine
Для реализации любой цифровой системы необходимы три основных компонента: комбинационная логика для вычисления функций с битами, элементы памяти для хранения битов и сигналы синхронизации для управления периодами обновления элементов памяти.
Конвертация десятичных чисел в двоичные
Каждая позиция (бит) в двоичном числе имеет свой "вес" — степень двойки. Сумма "весов" всех единичных битов и дает десятичное число.
Для 8-ми битного числа без знака, все биты кодируют число, количество комбинаций в 8-ми ячейках 256 (вместе с нулем)
Число 0 относится к беззнаковому типу.
| Бит/степень двойки | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
|---|---|---|---|---|---|---|---|---|
| Вес | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
0000_0000 = 0 # минимальное
0000_0001 = 2⁰ = 1
0000_0010 = 2¹ = 2
0000_0100 = 2² = 4
0000_0101 = 2² + 2⁰ = 5
1000_0000 = 2⁷ = 127
1111_1111 = 2⁷ + 2⁶ + 2⁵ + 2⁴ + 2³ + 2² + 2¹ + 2⁰ = 128 + 64 + 32 + 16 + 8 + 4 + 2 + 1 = 255 # максимальное
Для 8-ми битного числа со знаком, старший бит по мимо значения еще кодирует и знак, так если старший бит 0 это кодирует положительно число с весом 0, а 1 отрицательное и имеет вес -128 так как 2⁷=128
Количество комбинаций 256:
- Отрицательные (-128 … -1) → 128 комбинаций
- Положительные и ноль (0 … 127) → 128 комбинаций
Диапазон i8 типа: -128 … +127
Старший бит 0 кодирует положительное число, а 1 отрицательное
0 00000000
1 00000001
2 00000010
...
125 01111101
126 01111110
127 01111111 # до этого момента битовые представление чисел со знаком и без совпадали
-128 10000000 # старший бит стал 1 что означает отрицательное число, при чем по соглашению максимальное
-127 10000001
-126 10000010
...
-2 11111110
-1 11111111
0 00000000
| Бит/степень двойки | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
|---|---|---|---|---|---|---|---|---|
| Вес | -128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
01111111 = 2⁶ + 2⁵ + 2⁴ + 2³ + 2² + 2¹ + 2⁰ = 64 + 32 + 16 + 8 + 4 + 2 + 1 = 127 # максимальное
11111111 = 2⁷ + 2⁶ + 2⁵ + 2⁴ + 2³ + 2² + 2¹ + 2⁰ = -128 + 64 + 32 + 16 + 8 + 4 + 2 + 1 = -1
10000000 = 2⁷ = -128 # минимальное
10000001 = 2⁷ + 2⁶ = -128 + 1 = -127
fn main() { for x in i8::MIN..=i8::MAX { let bits = x as u8; println!("{:>4} = {:08b}", x, bits); } }
Для перевода отрицательного числа в двоичный, используют подход - дополнительный код еще его называют дополнением до двух (Two’s complement). Так как сперва дополнение до 1 при реверсе, а потом еще дополнение до 1 при прибавлении 1
Two’s complement позволяет использовать один и тот же сумматор для знаковых и беззнаковых чисел. Что бы сложение и вычитание работали без условий на знак.
Нужно:
- перевести положительное число в двоичную систему
- потом поменять нули на единицы и единицы на нули
- затем прибавить к результату 1
Например для -125
- положительное 125 в двоичной системе: 01111101
- реверс : 10000010
- прибавить 1 : 10000011
Можно проверить:
- 256 - 125 = 131 в двоичном виде 10000011 что соответствует двоичному представлению для отрицательно числа -125
Double trouble
Задача: Имеем 4 входа, получить на выходе 1 если два или более входа имеют 1
Это просто проверка: есть хотя бы одна пара единиц.
Когда у нас есть k состояний и n входов, это декартово произведение состояний, считается
= k состояний ^ n входов.Например функция принимает 4 типа enum, который имеет три состояния, то декартово произведение состояний:
3 × 3 × 3 × 3 = 3⁴ = 81.
В задаче имеем 4 входа с двумя состояними 0 или 1, следовательно декартово произведение состояний: 2 × 2 × 2 × 2 = 2⁴ = 16.
fn and(a: u8, b: u8) -> u8 { a & b } fn or(a: u8, b: u8) -> u8 { a | b } fn rule(a: u8,b: u8,c: u8,d: u8)->u8{ let total: u8 = a +b +c +d; return if total > 1 {1}else{0}; } fn solution1(a: u8,b: u8,c: u8,d: u8)->u8{ let prep1 = and(or(a, b), or(c, d)); let prep2 = or(prep1, and(a,b)); or(prep2, and(c, d)) } /* (a&b) | (a&c) | (a&d) | (b&c) | (b&d) | (c&d) */ fn solution2(a: u8,b: u8,c: u8,d: u8)->u8{ or( or( or( and(a, b), and(a, c) ), or( and(b, c), and(b, d) ) ), or( and(a, d), and(c, d) ) ) } fn main() { let states = [0, 1]; println!("ABCD expected sol1 sol2"); for &a in &states { for &b in &states { for &c in &states { for &d in &states { println!("{}{}{}{} {} {} {}", a, b, c, d, rule(a, b, c, d), solution1(a, b, c, d), solution2(a, b, c, d)); assert_eq!(rule(a, b, c, d), solution1(a, b, c, d)); assert_eq!(rule(a, b, c, d), solution2(a, b, c, d)); } } } } }
Odd number of signals
Нечетное число сигналов.
Задача: Имеем 4 входных сигнала.
Используя не более трех компонентов (
xnor,xor,nor,nand,or,and,not,on,off), установить вывод в значение 1, когда количество вводов со значением 1 нечетное.
Т.е. при четном числе входов со значением 1 нужно получить 0. Такая ситуация при которой имея два входа по 1 (т.е. четное) дают на выходе 0,а другая комбинация c 1 (не четная) дает выход 1, напоминает таблицу истинности для XOR
| XOR | 0 | 1 |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 1 | 0 |
fn xor(a: u8, b: u8) -> u8 { a ^ b} fn rule(a: u8,b: u8,c: u8,d: u8)->u8{ let total: u8 = a +b +c +d; return if total %2==0 {0}else{1}; } fn solution1(a: u8,b: u8,c: u8,d: u8)->u8{ xor( xor(a,b), xor(c,d) ) } fn main() { let states = [0, 1]; println!("ABCD expected sol1"); for &a in &states { for &b in &states { for &c in &states { for &d in &states { println!("{}{}{}{} {} {} ", a, b, c, d, rule(a, b, c, d), solution1(a, b, c, d)); assert_eq!(rule(a, b, c, d), solution1(a, b, c, d)); } } } } }
Counting signals
Задача: Вывод — двоичный счётчик, у которого каждый из трёх контактов соответствует числам 1, 2 и 4. Для подсчета входов в состоянии 1 увеличивайте счетчик.
Это означает:
- у нас 3 выходных пина
- они представляют биты двоичного числа
Мы хотим получить число единиц на входах: 0, 1, 2, 3 или 4
И вывести это число в двоичном виде тремя битами:
000 = 0
001 = 2^0 = 1
010 = 2^1 = 2
011 = 2^1 + 2^0 = 3
100 = 2^2 = 4
101 = 2^2 + 2^0 = 5
110 = 2^2 + 2^1 = 6
111 = 2^2 + 2^1 + 2^0 = 4 + 2 + 1 = 7
Т.е. выход — это 3-битное число от 0 до 7
Подсказка:
- схема для бита 1 такая же как и в уровне "Odd number of signals"
- Бит 1 (вес = 1) = 1, если количество входов 1 нечётное
- схема для бита 2 такая же как и в уровне "Double trouble"
- но случай при входе 1111 наоборот должен дать 0 на выходе, иначе неверное число закодируем
- бит 2 (вес = 2) = 1, если количество входов
1 ≥ 2 < 4 - так как bit4 = 1 только для входа 1111, то мы можем вычесть его из bit2:
bit2 = bit2 & !bit4
- Бит 4 (вес = 4) = 1 только если все входы = 1
Схема для Бит 4:
a ─┐
&──┐
b ─┘ &──┐
&── bit4
c ─┐ &──┘
&──┘
d ─┘
Строим три логических функции, каждая выдаёт бит результата:
| бит | правило | смысл |
|---|---|---|
| bit1 | odd_number_of_signals (XOR всех входов) | 1, если количество единиц нечётное |
| bit2 | double_trouble (≥2 единиц) | 1, если число единиц ≥2, но не 4 (& !bit4) |
| bit4 | and(a,b,c,d) | 1, если все единицы, иначе 0 |
Counting Signals — это задача на построение счётчика, который увеличивается только когда входной сигнал равен 1.
important
Для этого мы подбираем логические функции для каждого бита, чтобы они соответствовали таблице истинности
Иногда нужно подправить крайний случай (например, 1111 для bit2), чтобы результат строго совпадал с таблицей
Но можно придумать и другие логические функции, главное, чтобы по таблице истинности они давали те же значения на всех 16 комбинациях (декартово произведение 2⁴)
Мы не считаем напрямую, а имитируем таблицу истинности логикой, с возможной коррекцией крайних случаев.
Наши функции должны соответвовать такому поведению согласно таблицы, что бы двоичное представление числа равнялось числу входов 1
| a b c d | # единиц | bit4 | bit2 | bit1 | value = bit44 + bit22 + bit1*1 |
|---|---|---|---|---|---|
| 0 0 0 0 | 0 | 0 | 0 | 0 | 0 |
| 0 0 0 1 | 1 | 0 | 0 | 1 | 1 |
| 0 0 1 0 | 1 | 0 | 0 | 1 | 1 |
| 0 0 1 1 | 2 | 0 | 1 | 0 | 2 |
| 0 1 0 0 | 1 | 0 | 0 | 1 | 1 |
| 0 1 0 1 | 2 | 0 | 1 | 0 | 2 |
| 0 1 1 0 | 2 | 0 | 1 | 0 | 2 |
| 0 1 1 1 | 3 | 0 | 1 | 1 | 3 |
| 1 0 0 0 | 1 | 0 | 0 | 1 | 1 |
| 1 0 0 1 | 2 | 0 | 1 | 0 | 2 |
| 1 0 1 0 | 2 | 0 | 1 | 0 | 2 |
| 1 0 1 1 | 3 | 0 | 1 | 1 | 3 |
| 1 1 0 0 | 2 | 0 | 1 | 0 | 2 |
| 1 1 0 1 | 3 | 0 | 1 | 1 | 3 |
| 1 1 1 0 | 3 | 0 | 1 | 1 | 3 |
| 1 1 1 1 | 4 | 1 | 0 | 0 | 4 |
fn xor(a: u8, b: u8) -> u8 { a ^ b} fn and(a: u8, b: u8) -> u8 { a & b } fn or(a: u8, b: u8) -> u8 { a | b } fn not(x: u8) -> u8 {!x & 1} fn odd_number_of_signals(a: u8,b: u8,c: u8,d: u8)->u8{ xor( xor(a,b), xor(c,d) ) } fn double_trouble(a: u8,b: u8,c: u8,d: u8)->u8{ let prep1 = and(or(a, b), or(c, d)); let prep2 = or(prep1, and(a,b)); or(prep2, and(c, d)) } fn calculate_bit4(a: u8,b: u8,c: u8,d: u8)->u8{ and(and(a, b), and(c, d)) } fn rule(a: u8,b: u8,c: u8,d: u8)->u8{ a + b + c + d } fn solution(a: u8,b: u8,c: u8,d: u8)->u8{ let bit1 = odd_number_of_signals(a, b, c, d); let mut bit2 = double_trouble(a, b, c, d); let bit4 = calculate_bit4(a, b, c, d); bit2 = and(bit2, not(bit4));// mask, чтобы 1111 не давало бит2 bit1*1 + bit2*2 + bit4*4 // умножаем на вес // или через сдвиги // из трёх бит (bit1, bit2, bit4) собрать одно число, соответствующее весам 1, 2, 4 //bit1 + (bit2 << 1) + (bit4 << 2) } fn main() { let states = [0, 1]; println!("ABCD expected sol | bit4 bit2 bit1"); for &a in &states { for &b in &states { for &c in &states { for &d in &states { println!("{}{}{}{} {} {} | {} {} {}", a, b, c, d, rule(a, b, c, d), solution(a, b, c, d), calculate_bit4(a, b, c, d), and(double_trouble(a, b, c, d), not(calculate_bit4(a, b, c, d))), odd_number_of_signals(a, b, c, d) ); assert_eq!(rule(a, b, c, d), solution(a, b, c, d)); } } } } }
Карта Карно
- Using REAL Computer Engineering Skills to Avoid Getting Eaten
- Karnaugh Maps (learnabout-electronics.org)
Карта Карно = таблица истинности, разложенная так, чтобы одинаковые случаи стояли рядом. Это нужно, чтобы видеть, какие входы можно “выкинуть” из формулы.
Карта Карно не считает. Она показывает:
- где входы можно игнорировать
- какие переменные не влияют на результат
Это просто упрощение таблицы истинности.
Карта Карно = визуальный способ получить odd_number_of_signals, double_trouble, mask
Карты Карно всегда строят для одного выхода
expected = Y2 Y1 Y0 (вес 4, 2, 1)
Поэтому мы делаем 3 отдельные карты для задачи Counting signals:
-
одну для Y0
-
одну для Y1
-
одну для Y2
Как выглядит карта Карно для 4 входов
Для 4 переменных делаем 4×4 таблицу.
- строки: AB
- столбцы: CD
- порядок — код Грея (чтобы отличался 1 бит)
CD
00 01 11 10
AB 00 . . . .
01 . . . .
11 . . . .
10 . . . .
Карта Карно для Y0 (младший бит)
Шаг 1: заполняем 1 там, где Y0 = 1
Y0 = 1, когда число единиц нечётное
CD
00 01 11 10
AB 00 0 1 0 1
01 1 0 1 0
11 0 1 0 1
10 1 0 1 0
Шаг 2: группируем
(шахматный узор, его нельзя упростить через AND/OR — это признак XOR)
Шаг 3: формула
Y0 = A ⊕ B ⊕ C ⊕ D
Это прямо видно из карты, а не берётся с потолка.
Карта Карно для Y2 (бит 4)
Шаг 1: Y2 = 1 ТОЛЬКО когда ABCD = 1111
CD
00 01 11 10
AB 00 0 0 0 0
01 0 0 0 0
11 0 0 1 0
10 0 0 0 0
Шаг 2: группируем
Группировать нечего → одиночная клетка
Шаг 3: формула
Y2 = A · B · C · D
Карта Карно для Y1 (бит 2)
Y1 = 1, когда:
- ровно 2 единицы
- ровно 3 единицы но не 4
CD
00 01 11 10
AB 00 0 0 1 0
01 0 1 0 1
11 1 0 0 1
10 0 1 1 0
Шаг 1: группируем по 2 и 4
получаем группы вида:
- AB
- AC
- AD
- BC
- BD
- CD
Шаг 2: выписываем формулу
Y1_raw = AB + AC + AD + BC + BD + CD
Шаг 3: убираем 1111
Карта показывает, что 1111 лишний → вычитаем его маской:
Y1 = Y1_raw · ¬(A·B·C·D)
Half Adder
Полусумматор/Бинарный сумматор.
При сложении двух двоичных цифр A и B бит суммы реализуется как XOR (Искл-ИЛИ).
| XOR | 0 | 1 |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 1 | 0 |
т.е.ситуация когда происходит переполнения, мы делаем перенос, поэтому при входе 11 на выходе 0, но 1 пойдет в перенос
А бит переноса — как AND.
| AND | 0 | 1 |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
Поэтому полусумматор реализуется вентилями XOR и AND.
Задача: Вычислите сумму Вводов(INPUTS) в двоичном формате, результат (SUM) будет 0 или 1. Как и в обычном сложении, если результат не помещается в один разряд, установите перенос разряда (CARRY) в значение 1.
fn xor(a: u8, b: u8) -> u8 { a ^ b } fn and(a: u8, b: u8) -> u8 { a & b } fn half_adder(a: u8, b: u8) -> (u8, u8) { let sum = xor(a, b); // бит суммы let carry = and(a, b); // бит переноса (sum, carry) } fn main() { for a in 0..=1 { for b in 0..=1 { let (s, c) = half_adder(a, b); println!("{} + {} -> sum={}, carry={}", a, b, s, c); } } }
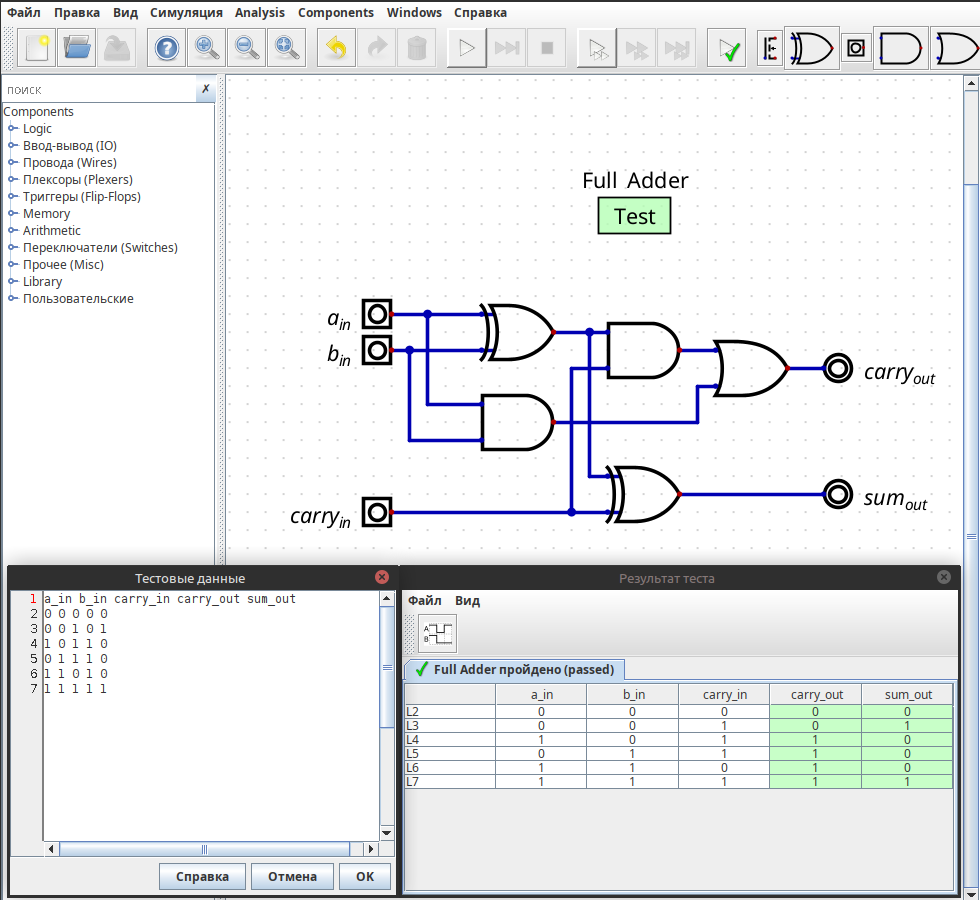
Full Adder
Полный сумматор/Тернарный сумматор.
Существует причина, по которой эта схема называется полусумматором. Разумеется, она складывает две двоичные цифры и выдает бит суммы и бит переноса. Однако длина подавляющего большинства двоичных чисел превышает один бит. То, что полусумматор не может сделать, так это прибавить возможный бит переноса, получившийся в результате предыдущей операции сложения.
Для сложения трех двоичных цифр понадобятся два полусумматора и вентиль ИЛИ
Задача: На предыдущем уровне мы суммировали значения двух Вводов, в этот раз мы будем суммировать три. В общем, сложите входные данные в двоичном формате, чтобы результат был либо 0 либо 1.
Как и при обычном сложении "столбиком", когда результат не может быть описан одной цифрой, установите перенос (CARRY) в значение 1.
fn xor(a: u8, b: u8) -> u8 { a ^ b } fn and(a: u8, b: u8) -> u8 { a & b } fn or(a: u8, b: u8) -> u8 { a | b } fn full_adder(a: u8, b: u8, cin: u8) -> (u8, u8) { let sum = xor(xor(a, b), cin); let carry = or( and(a, b), and(cin, xor(a, b)) ); (sum, carry) } fn main() { for a in 0..=1 { for b in 0..=1 { for cin in 0..=1 { let (s, c) = full_adder(a, b, cin); println!("{} {} {} -> sum={}, carry={}", a, b, cin, s, c); } } } }
В симуляторе Digital есть возможность зафиксировать свою реализацию компонента с помощью тестов.
Double the number
Удвоить число
Ввод и Вывод на этом уровне используют байты вместо битов. Один из двух новых компонентов умеет "разбирать" байт на биты (Byte Splitter), а второй наоборот "собирает" биты в байт (Byte Combiner).
Удвоение числа в двоичной системе — это сдвиг влево на 1 бит:
N = 0101011 (43)
2·N = 1010110 (86)
2·N = N << 1
Задача: Используя эти компоненты придумайте как удвоить число на Входе (число на входе не больше 127).
Byte Splitter 1 → Byte Combiner 2
Byte Splitter 2 → Byte Combiner 4
Byte Splitter 4 → Byte Combiner 8
Byte Splitter 8 → Byte Combiner 16
Byte Splitter 16 → Byte Combiner 32
Byte Splitter 32 → Byte Combiner 64
Byte Splitter 64 → Byte Combiner 128
Byte Splitter 128 → Byte Combiner 1
fn main() { let n: u8 = 117; // 01110101 let doubled = n << 1; // сдвиг влево на 1 бит → 234 = 11101010 println!("{:08b} n = {n}", n); println!("{:08b} doubled = {doubled}", doubled); }
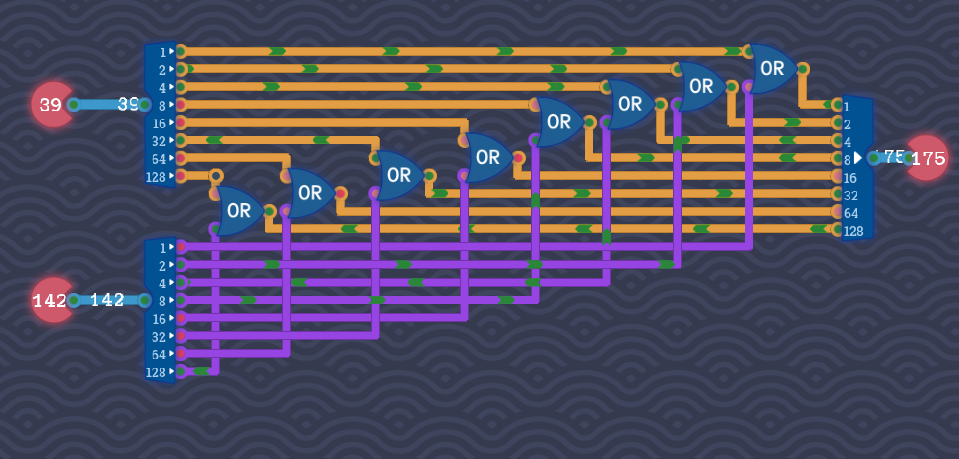
Byte OR
Задача: Применить операцию OR к целому байту т.е. побайтово применить gate OR
Byte NOT
tip
Разблокирует: компонент 8 bit NOT
Задача: Применить операцию NOT к целому байту т.е. побайтово применить gate NOT
... так же как и для byte OR, разбиваем байт на биты (Byte Splitter) и инвертируем бит, собираем обратно через Byte Combiner
Adding Bytes
tip
Разблокирует: компонент сложения байт
Суммируем байты.
Задача:
Сложите два входных байта. Каждый выходной бит должен быть результатом сложения соответствующих битов входных данных, а также, возможно, переноса.
Если результат не помещается в 8 бит, поверните перенос на выходе (можно считать его 9-м битом).
Наконец, есть еще и входной перенос. Он полезен для последовательного соединения сумматоров байтов для сложения больших чисел. Можно представить этот перенос как сложение 0 или 1.
Нам нужно 8 полных сумматоров.
Что дано в задаче
Входы
- Byte A — 8 бит: A0 … A7
- Byte B — 8 бит: B0 … B7
- Carry In — 1 бит (Cin)
Выходы
- Sum Byte — 8 бит: S0 … S7
- Carry Out — 1 бит (Cout)
- (это «9-й бит», если сумма > 255)
00000011 #3
+
00000011 #3
---------
00000110 #6
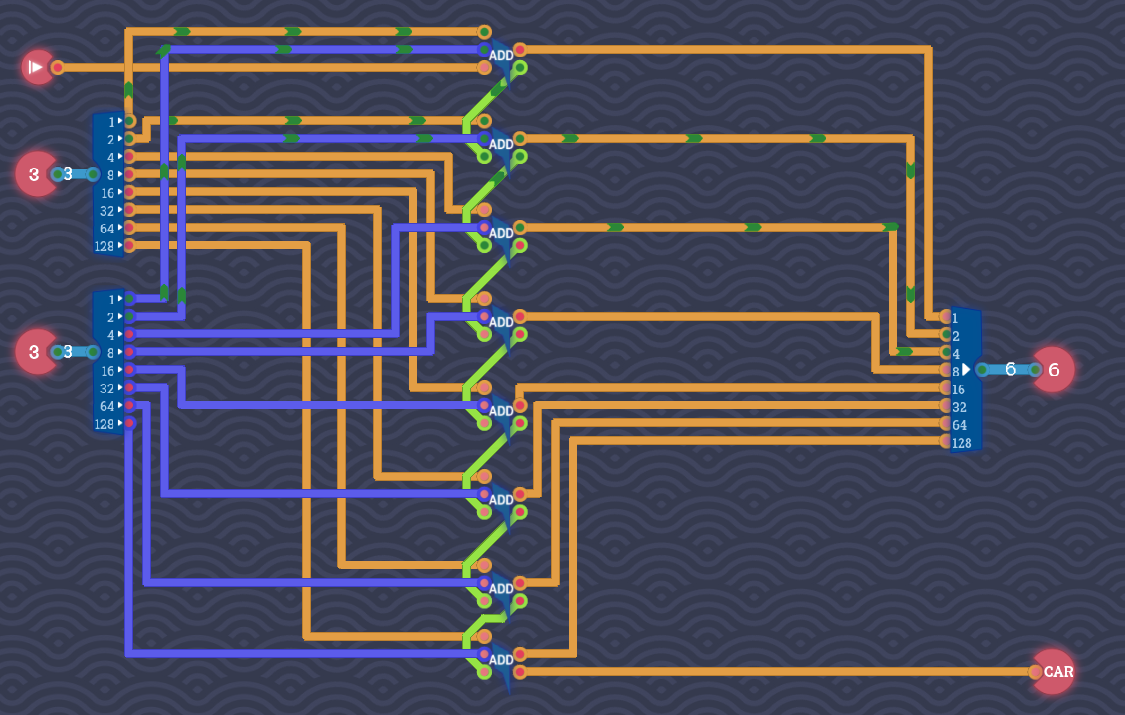
Параллельный многоразрядный сумматор:
Сумматор на 8 разрядов (www.falstad.com/circuit)
Negative Numbers
Отрицательные числа, для операций вычитания нужны отрицательные числа.
На этом уровне вводится "дополнительный код", наиболее распространенное представление отрицательных чисел.
Здесь старшая цифра инвертируется. Для байтов это означает, что 8-я цифра меняет свое значение со 128 на -128.
Этот уровень завершается, когда вы достигаете 3-го уровня или выше.
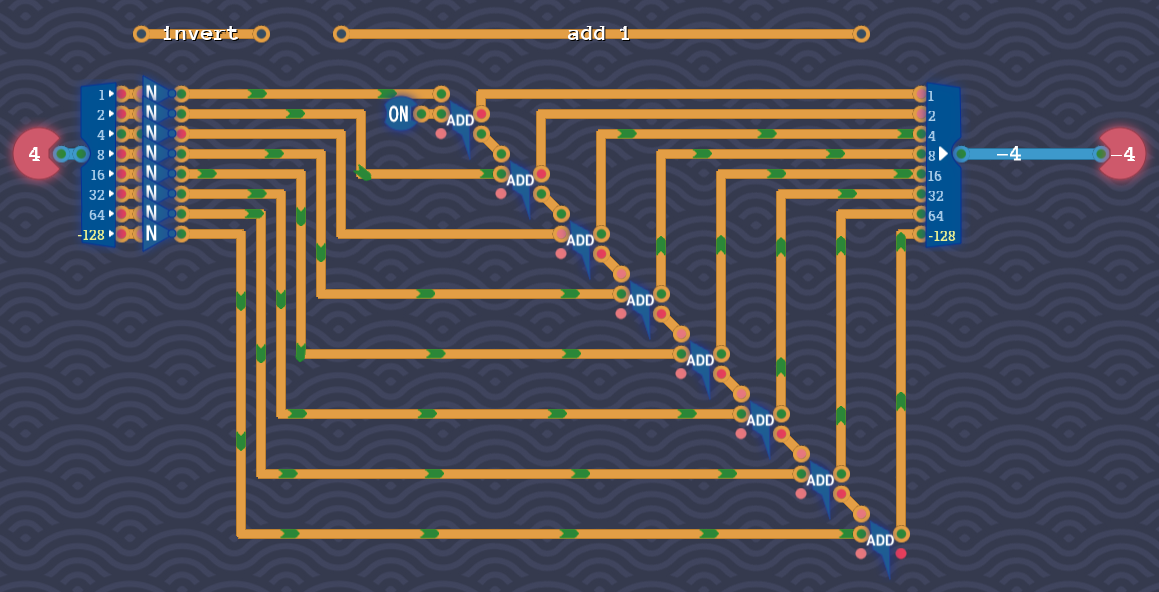
Signed Negator
tip
Разблокирует: компонент NEG инверсия знака (меняет положительное на отрицательное) для 8 бит.
Задача: Принимая входные данные как знаковые (где 8-й бит равен -128), создайте компонент, который принимает число и инвертирует его.
Например, если перевести 4 в отрицательное число, получится -4. Если перевести -9 в отрицательное число, получится 9.
Отрицание: A - B = A + (-B) для реализации вычитания через сложение нам нужно найти число -B по принципу B + (-B) = 0
Алгоритм получения отрицательного числа (наз. дополнительный код или дополнение до двух)
- Возьмите положительное число
- Инвертируйте все биты
- Прибавьте 1
0000_0100 # 4
1111_1011 # инвертируем
1111_1011
+ # прибавим 1
0000_0001
---------
1111_1100 #-4
fn main() { let x: u8 = 4; println!("{:08b} # {x}", x); let inverted = !x; println!("{:08b} # инвертируем", inverted); let twos_complement = inverted.wrapping_add(1); println!("{:08b} # прибавим 1", twos_complement); let result = twos_complement as i8; assert_eq!(result, -4i8); }
important
С точки зрения двоичной логики 8-битного процессора, вычесть 1, прибавить -1 и прибавить 255 (MAX) — это одна и та же операция.
fn invert(x: u8) -> i8{ let inv = !x; let twos_complement = inv.wrapping_add(1); twos_complement as i8 } fn main() { // С точки зрения двоичной логики 8-битного процессора, // вычесть 1, прибавить -1 и прибавить 255 — это одна и та же операция. let minuend: u8 = 9; // (Уменьшаемое) — то число, из которого вычитают let subtrahend: u8 = 1;// (Вычитаемое) — то число, которое вычитают // Способ 1 - просто вычесть println!("{}", minuend - subtrahend); // Способ 2 - прибавить инверсию let neg: i8 = invert(subtrahend); // инвертируем println!("{}", minuend as i8 + neg); // Способ 3 - прибавить максимальное значение типа для переполнения //println!("{}", minuend + 255); // Error arithmetic_overflow println!("{}", minuend.wrapping_add(u8::MAX));// разрешаем циклическое переполнение //--------------------------------------------------------------------------------- // Еще пример вычитания способом 3. // Вычтим из 9 число 7 let minuend: u8 = 9; // (Уменьшаемое) let subtrahend: u8 = 7;// (Вычитаемое) // прибавить 255 (u8::MAX) эвивалентно вычитанию 1 // прибавить 254 эвивалентно вычитанию 2 // прибавить 253 эвивалентно вычитанию 3 // ... и т.д println!("{}",minuend.wrapping_add(u8::MAX-(subtrahend-1)));// 2 }
Coder или encoder (шифратор)
Логическая схема, которая преобразует номер активного входа (уровень HIGH может быть только у одного из входов) в двоичный код.
Шифратор — это комбинационная логическая схема, которая: принимает 2ⁿ входов, выдаёт n выходов, кодирует индекс активного входа.
Например закодируем числа 0-9 в двоичный код. Тогда мы имеем 10 входов и минимум 4 выхода (2⁴ = 16 ≥ 10) (так как мы имея 4 выхода можем закодировать числа 0-15 т.е. 16 чисел но реализуем только 10 из них то наз. это неполным кодером)
Формулы:
0 = I1 OR I3 OR I5 OR I7 OR I9
1 = I2 OR I3 OR I6 OR I7
2 = I4 OR I5 OR I6 OR I7
3 = I8 OR I9
Как получить формулы:
Смотрим на двоичное представление кодируемого входа
N pos 3 2 1 0
--------------
0 0 0 0 0
1 0 0 0 1
2 0 0 1 0
3 0 0 1 1
4 0 1 0 0
5 0 1 0 1
6 0 1 1 0
7 0 1 1 1
8 1 0 0 0
9 1 0 0 1
Смотрим только HIGH уровень в расчитываемой позиции бита выхода.
Для позиции 0 (т.е. первый младший бит) на выходах с HIGH уровнем только вход для 1,3,5,7,9
Для позиции 1 на выходах с HIGH уровнем только вход для 2,3,6,7
Для позиции 2 на выходах с HIGH уровнем только вход для 4,5,6,7
Для позиции 4 на выходах с HIGH уровнем только вход для 8,9
note
реальная микросхема шифратора К155ИВ1 8806
Decoder (дешифратор)
Decoder — это схема, которая превращает бинарное число в один выход.
Количество выходов 2ⁿ где n это число входов.
Например декодируем 4 бита в диапазон чисел от 0-9.
Как получить формулы:
Каждый выход - это AND всех входов,
где:
бит 1 → прямой вход
бит 0 → инверсия входа
Для выхода 9 смотрим его декодирующий бинарный вид 1001
pos_3 1
pos_2 0
pos_1 0
pos_0 1
Переводим в формулу, все входы с 0 инфертируем: pos_3 AND NOT pos_2 AND NOT pos_1 AND pos_0
Декодер 4 на 10 (неполный декодер)
p.s. схему можно упростить, уменьшив количество элементов NOT. Необходимо создать для каждого входа инверсионный аналог через NOT, тогда не нужно будет для каждого gate AND использовать собственное отрицание, а просто подключится к нужной линии.
1 Bit Decoder
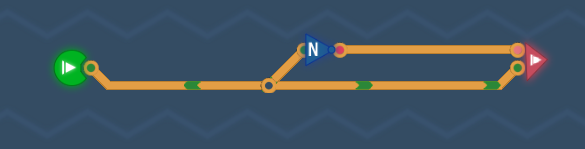
Decoder "1 to 1"
Задача: Создайте компонент, который сможет переключать "поток" между двумя контактами.
3 Bit Decoder
Decoder "3 to 8"
С 3-мя входными битами: A, B, C, возможны 8 комбинаций выхода: 2³ = 8.
Задача:
Создайте схему которая выбирает один выходной бит для каждой из 8-и комбинаций.
Строго один бит должен быть положительным для каждой из комбинаций.
Нужно сделать так, чтобы, для каждой комбинации ABC, был ровно один выход был 1, остальные 0
Когда у нас есть k состояний и n входов, это декартово произведение состояний, считается: N = k состояний ^ n входов
У нас есть два состояния 0 либо 1 т.е. k=2. И 3 входа n=3, получаем N=2^3=8
Все 8 уникальных комбинаций мы можем придумать в произвольном порядке, но в задаче есть таблица истинности, которой мы будем следовать. И к тому же в таком же порядке следования opcode кодируются числа 1,2,3...
A B C | Активный выход
---------------------
0 0 0 | 00000001 D0
0 0 1 | 00000010 D1
0 1 0 | 00000100 D2
0 1 1 | 00001000 D3
1 0 0 | 00010000 D4
1 0 1 | 00100000 D5
1 1 0 | 01000000 D6
1 1 1 | 10000000 D7
Нам нужно переключаться между выходными битами в зависимости от числа, соответсующего входному биту
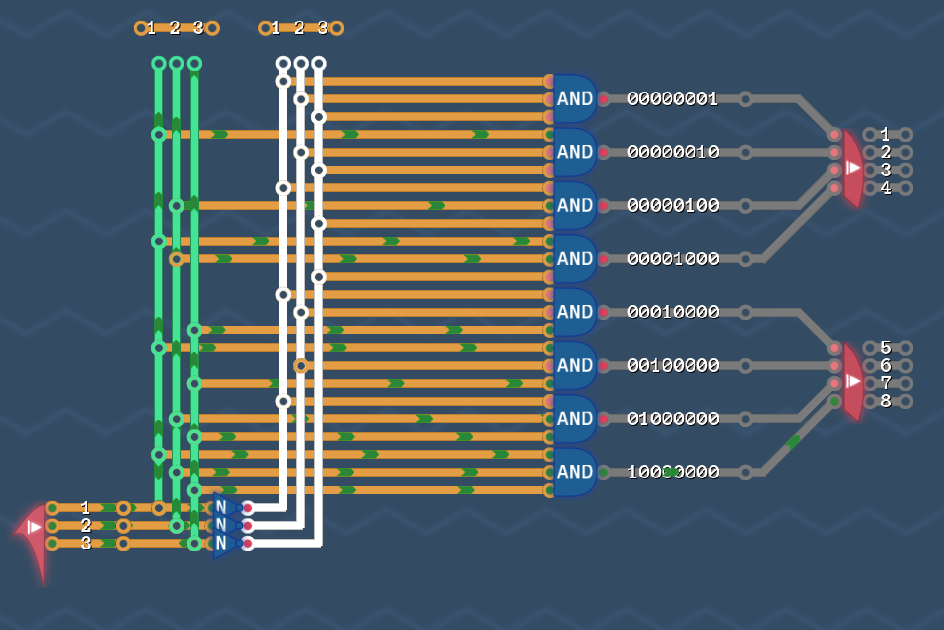
Или с помощью открытого компонента 1 Bit Decoder
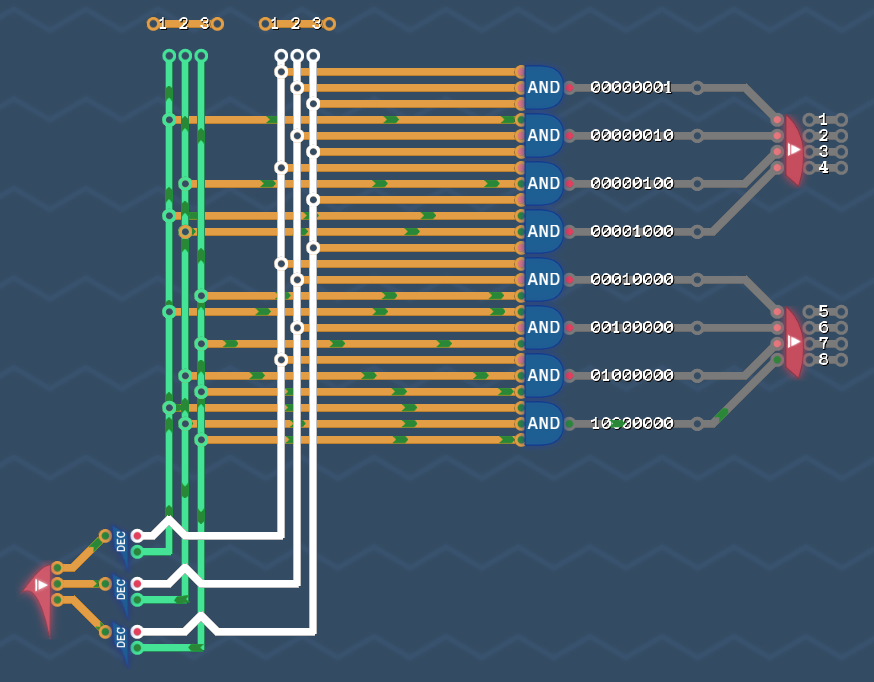
Logic Engine
tip
Разблокирует компоненты: 8 bit AND, 8 bit NAND, 8 bit NOR
strategywiki.org/wiki (Logic Engine)
Задача:
Создайте устройство, способное выполнять операции OR, NAND, NOR или AND с двумя восьмибитными входами.Третий вход будет 8-ми битной инструкцией. Инструкция — это просто число, определяющее, что нужно вычислить:
0 OR 1 NAND 2 NOR 3 ANDт.е. нам хватит всего первых двух младших битов
00 OR 01 NAND 10 NOR 11 AND
Это то же самое, что и создание ИЛИ, НЕ-И, НЕ-ИЛИ, И в начале, только с 8-битными компонентами.
Таблицы истинности четырех основных логических элементов симметричны. Преобразование между ними можно осуществить путем инвертирования входного сигнала ( NAND ⇄ OR, AND ⇄ NOR ):
-
Что бы получить OR мы можем инвертировать оба входа в NAND и получить на его выходе эквивалент OR.
-
Что бы получить NOR мы можем инвертировать оба входа в AND и получить на его выходе эквивалент AND.
Или инвертирования выходного сигнала ( OR ⇄ NOR,NAND ⇄ AND ):
-
Что бы получить NOR мы можем инвертировать выход OR и получить сразу NOR.
-
Что бы получить AND мы можем инвертировать выход NAND и получить сразу AND.
Учитывая что на этом уровне нам еще не открыты восьмибитные NAND, AND то мы можем использовать восьмибитный OR.
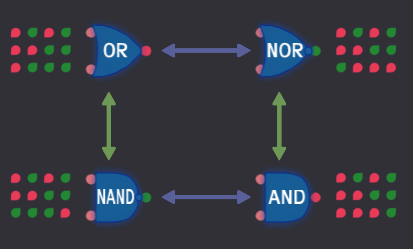
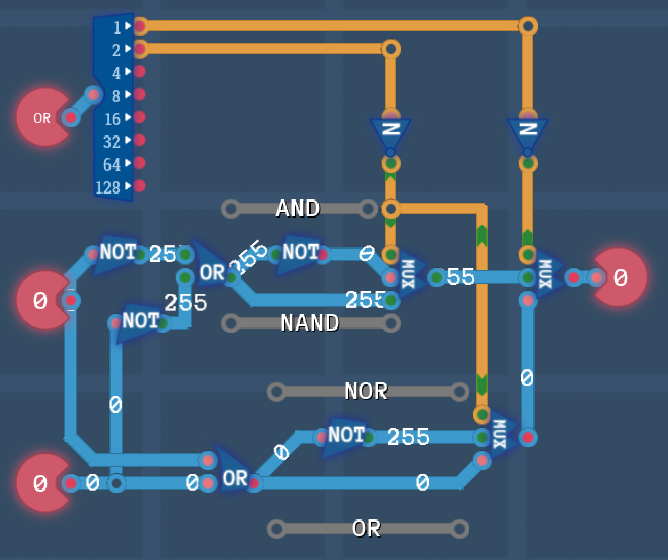
Если бы были доступны NAND и AND то можно было бы использовать схему аналогичную этой:
8 bit NAND